Extended Kalman filter example in R

Last week’s post about the Kalman filter focused on the derivation of the algorithm. Today I will continue with the extended Kalman filter (EKF) that can deal also with nonlinearities. According to Wikipedia the EKF has been considered the de facto standard in the theory of nonlinear state estimation, navigation systems and GPS.

Kalman filter

I had the following dynamic linear model for the Kalman filter last week:

\[ \begin{aligned} x_{t+1} & = A x_t + w_t,\quad w_t \sim N(0,Q)\\ y_t &=G x_t + \nu_t, \quad \nu_t \sim N(0,R)\\ x_1 & \sim N(\hat{x}_0, \Sigma_0) \end{aligned} \]

With \(x_t\) describing the state space evolution, \(y_t\) the observations, \(A, Q, G, R, \Sigma_0\) matrices of appropriate dimensions, \(w_t\) the evolution error and \(\nu_t\) the observation error. The Kalman filter provides recursive estimators for \(x_t\) via:

\[ \begin{aligned} K_{t} &= A \Sigma_t G' (G \Sigma_t G' + R)^{-1}\\ \hat{x}_{t+1} &= A \hat{x_t} + K_{t} (y_t - G \hat{x}_t) \\ \Sigma_{t+1} &= A \Sigma_t A' - K_{t} G \Sigma_t A' + Q \end{aligned} \]

In the case of nonlinearities on the right hand side of either the state (\(x_t\)) or observation (\(y_t\)) equation the extended Kalman filter uses a simple and elegant trick: Taylor series of the first order, or in other words, I simply linearise the right hand side. The matrices \(A\) and \(G\) will be the Jacobian matrices of the respected vector functions.

Logistic growth

As an example I will use a logistic growth model, inspired by the Hakell example given by Dominic Steinitz.

The logistic growth model can be written as a time-invariant dynamical system with growth rate \(r\) and carrying capacity \(k\): \[ \begin{aligned} \dot{p} & = r p\Big(1 - \frac{p}{k}\Big) \end{aligned} \] The above ordinary differential equation has the well known analytical solution:

\[ p = \frac{kp_0\exp(r\,t)}{k + p_0(\exp(r\,t) - 1)} \]

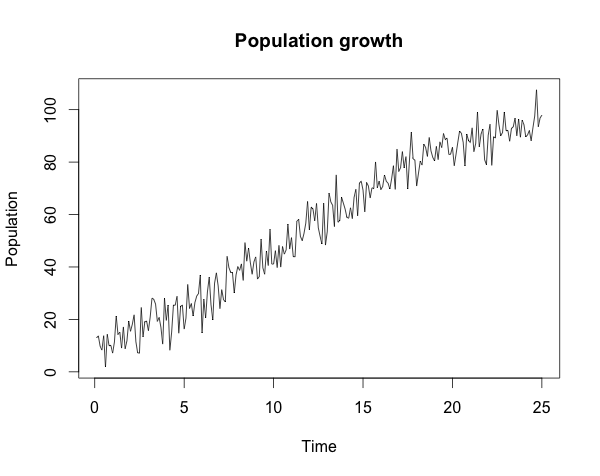
Suppose I observe data of a population for which I know the carrying capacity \(k\), but where the growth rate \(r\) is noisy.

Extended Kalman filter

The state space and observation model can then be written as: \[ \begin{aligned} r_i &= r_{i-1} \\ p_i &= \frac{kp_{i-1}\exp(r_{i-1}\Delta T)}{k + p_{i-1}(\exp(r_{i-1}\Delta T) - 1)} \\ y_i &= \begin{bmatrix}0 & 1\end{bmatrix} \begin{bmatrix}r_i \\ p_i\end{bmatrix} + \nu \end{aligned} \]

Or with \(x_i:=\begin{bmatrix}r_i & p_i\end{bmatrix}'\) as:

\[ \begin{aligned} x_i &= a(x_i)\\ y_i &= G x_i + \nu_i\\ \nu_i & \sim N(0,R) \end{aligned} \]

In my example the state space model is purely deterministic, so there isn’t any evolution noise and hence \(Q=0\).

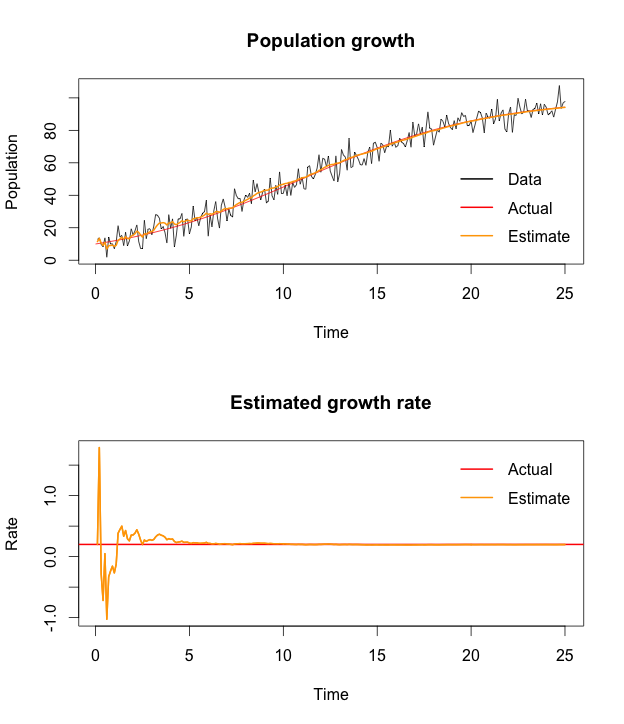
With an initial prior guess for \(x_0\) and \(\Sigma_0\) and I am ready to go. The R code below shows my implementation with the algorithm above. Note that I use the jacobian function of the numDeriv package.After a few time steps the extended Kalman filter does a fantastic job in reducing the noise. Perhaps this shouldn’t be too surprising as a local linearisation of the logistic growth function will give a good fit. The situation might be different for highly nonlinear functions. The Wikipedia article about the Kalman filter suggests the unscented version in those cases.

R code

Session Info

R version 3.1.2 (2014-10-31)
Platform: x86_64-apple-darwin13.4.0 (64-bit)

locale:
[1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8

attached base packages:
[1] stats graphics grDevices utils datasets methods base     

other attached packages:
[1] numDeriv_2012.9-1

loaded via a namespace (and not attached):
[1] tools_3.1.2