How cold is it? A Bayesian attempt to measure temperature

It is getting colder in London, yet it is still quite mild considering that it is late November. Well, indoors it still feels like 20°C (68°F) to me, but I have been told last week that I should switch on the heating.

Luckily I found an old thermometer to check. The thermometer showed 18°C. Is it really below 20°C?

The thermometer is quite old and I’m not sure that is works properly anymore. So, what shall I do now? Perhaps I should consider that both measurements are uncertain and try to combine them.

I believe that I can sense the temperature within ±3°C, while I think that the thermometer still works within ±2°C. Assuming that both measurements follow a Gaussian (Normal) distribution, with the uncertainties given as standard deviations, I can use Bayes’ theorem to combine my hypothesis with the data. The posterior distribution will be Gaussian again with conjugated hyper-parameters: \[ \mu=\left.\left(\frac{\mu_0}{\sigma_0^2} + \frac{\sum_{i=1}^n x_i}{s^2}\right)\right/\left(\frac{1}{\sigma_0^2} + \frac{n}{s^2}\right) \\\\\\ \sigma^2=\left(\frac{1}{\sigma_0^2} + \frac{n}{s^2}\right)^{-1} \]With $K := $ this simplifies to: \[ \mu = K\, \bar{x} + (1 - K)\, \mu_0 \mbox{, with } \bar{x}=\frac{1}{n}\sum_{i=1}^n x_i\\\\\\ \sigma = s \,\sqrt{K/n} \]In my case I have: \(n=1,\; x_1=18^{\circ}C,\; s=2^{\circ}C,\; \mu_0=20^{\circ}C,\; \sigma_0=3^{\circ}C\).

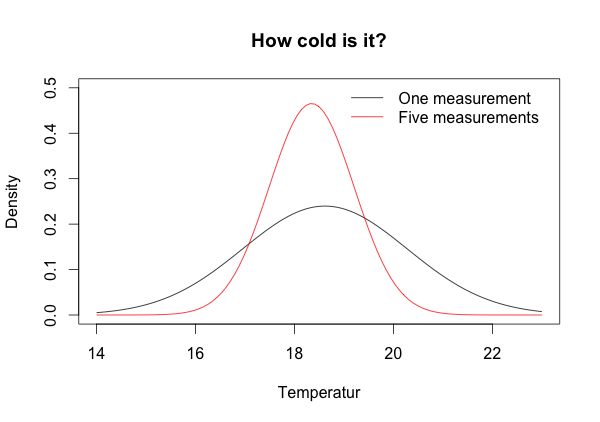
Hence, the posterior distribution has parameters \(\mu=18.6^{\circ}C\) and \(\sigma=1.7^{\circ}C\). Thus, my best guess would be that is actually a little colder than I thought. One could argue that the probability that is below 20° is 80%.

Over the last five days my perception of the temperature didn’t change, neither did the weather forecast, but the measurements showed: 18°C, 19°C, 17.5°C, 18°C, 18.5°C.

With that information the parameters update to \(\mu=18.3^{\circ}C\) and \(\sigma=0.9^{\circ}C\). I can’t deny it any longer it has got colder. The probability that is below 20°C is now at 97% and the heating is on.

Without any prior knowledge I may have used a t-test to check the measurements. But here I believe that I have information about the thermometer and my own temperature sensing abilities which I don’t want to ignore.

R code

Session Info

R version 3.1.2 (2014-10-31)
Platform: x86_64-apple-darwin13.4.0 (64-bit)

locale:
[1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
[1] BayesianFirstAid_0.1 rjags_3-14           coda_0.16-1         
[4] lattice_0.20-29     

loaded via a namespace (and not attached):
[1] grid_3.1.2    MASS_7.3-35   mnormt_1.5-1  stringr_0.6.2