Approximating the impact of inflation

The other day someone mentioned to me a rule of thumb that he was using to estimate the number of years \(n\) it would take for inflation to destroy half of the purchasing power of today’s money: \[ n = \frac{70}{p}\] Here \(p\) is the inflation in percent, e.g. if the inflation rate is \(2\%\) then today’s money would buy only half of today’s goods and services in 35 years. You can also think of a saving account with an interest rate of \(2\%\) that would double your money in 35 years.

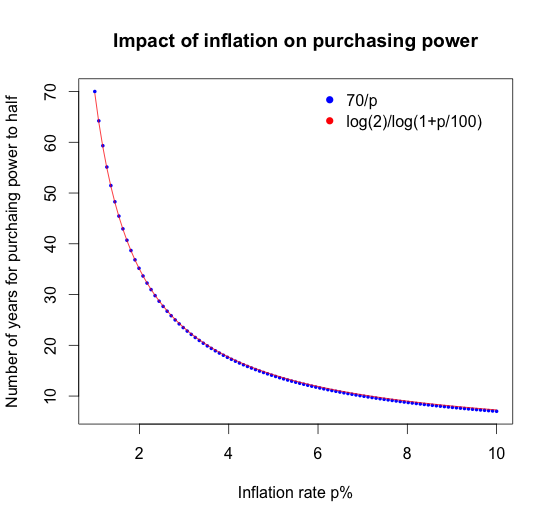
It is not difficult to derive this formula. The starting point is: \[ 2K = K (1 + \frac{p}{100})^n \] This is equivalent to: \[ 2 = (1 + \frac{p}{100})^n \] Taking the log gives: \[ \log(2) = n \log(1 + \frac{p}{100}) \] The first term of the Taylor series approximation of \(\log(1+x)\) for small \(x\) is \(x\). Hence for small \(p\) I can set: \[ \log(2) \doteq n \, \frac{p}{100} \] Next I have to estimate the value for \(\log(2)\). Writing it as an integral leads to: \[ \log(2) = \int_1^2 \frac{1}{x} \,dx \] Using Simpson’s rule I can approximate the integral with: \[ \int_1^2 \frac{1}{x} \,dx \doteq \frac{2-1}{6} (1+4\frac{2}{1+2}+\frac{1}{2} ) = \frac{25}{36} \doteq 0.7 \] Thus, \[ n \doteq \frac{70}{p} \] Plotting the two formulas against each other reveals that the approximation works pretty well, even for inflation rates up to 10%.

R Code

Here is the R code to reproduce the plot.

curve(70/x, from=1, to=10, 
      xlab="Inflation rate p%", 
      ylab="Number of years for purchaing power to half", 
      main="Impact of inflation on purchasing power",
      col="blue", 
      type="p", pch=16, cex=0.5)
curve(log(2)/(log(1+x/100)), 
      from=1, to=10, add=TRUE, 
      col="red")
legend("topright", 
       legend=c("70/p","log(2)/log(1+p/100)"), 
       bty="n",
       col=c("blue", "red"), 
       pch=c(16,16), pt.cex=c(1,1))