Logistic map: Feigenbaum diagram in R

The other day I found some old basic code I had written about 15 years ago on a Mac Classic II to plot the Feigenbaum diagram for the logistic map. I remember, it took the little computer the whole night to produce the bifurcation chart.

With today’s computers even a for-loop in a scripting language like R takes only a few seconds.

logistic.map <- function(r, x, N, M){
  ## r: bifurcation parameter
  ## x: initial value
  ## N: number of iteration
  ## M: number of iteration points to be returned
  z <- 1:N
  z[1] <- x
  for(i in c(1:(N-1))){
    z[i+1] <- r *z[i]  * (1 - z[i])
  }
  ## Return the last M iterations 
  z[c((N-M):N)]
}

## Set scanning range for bifurcation parameter r
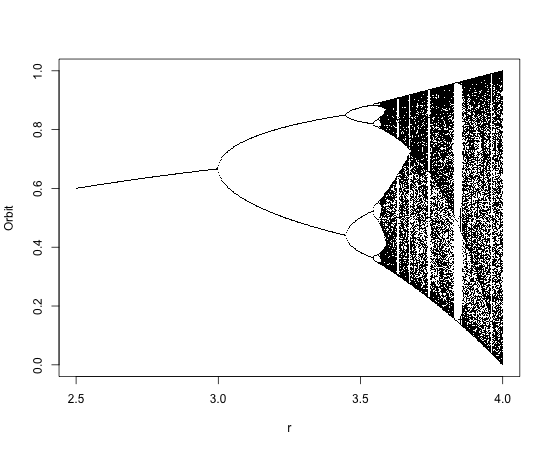
my.r <- seq(2.5, 4, by=0.003)
system.time(Orbit <- sapply(my.r, logistic.map,  x=0.1, N=1000, M=300))
##   user  system elapsed (on a 2.4GHz Core2Duo)
##   2.910   0.018   2.919 

Orbit <- as.vector(Orbit)
r <- sort(rep(my.r, 301))

plot(Orbit ~ r, pch=".")

Let’s not forget when Mitchell Feigenbaum started this work in 1975 he did this on his little calculator!

Update, 18 March 2012

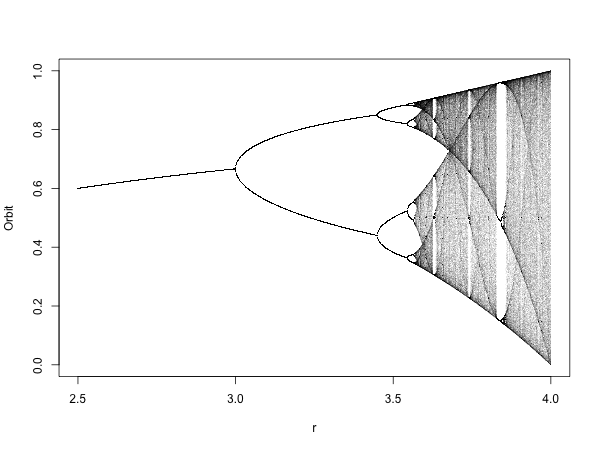
The comment from Berend has helped to speedup the code by a factor of about four, thanks to byte compiling (using the same parameters as above), and Owe got me thinking about the alpha value of the plotting colour. Here is the updated result, with the R code below:

library(compiler) ## requires R >= 2.13.0
logistic.map <- cmpfun(logistic.map) # same function as above
my.r <- seq(2.5, 4, by=0.001)
N <- 2000; M <- 500; start.x <- 0.1
orbit <- sapply(my.r, logistic.map,  x=start.x, N=N, M=M)
Orbit <- as.vector(orbit)
r <- sort(rep(my.r, (M+1)))
plot(Orbit ~ r, pch=".", col=rgb(0,0,0,0.05))