Fitting distributions with R

Fitting distribution with R is something I have to do once in a while, but where do I start?

A good starting point to learn more about distribution fitting with R is Vito Ricci’s tutorial on CRAN. I also find the vignettes of the actuar and fitdistrplus package a good read. I haven’t looked into the recently published Handbook of fitting statistical distributions with R, by Z. Karian and E.J. Dudewicz, but it might be worthwhile in certain cases, see Xi’An’s review. A more comprehensive overview of the various R packages is given by the CRAN Task View: Probability Distributions, maintained by Christophe Dutang.

How do I decide which distribution might be a good starting point?

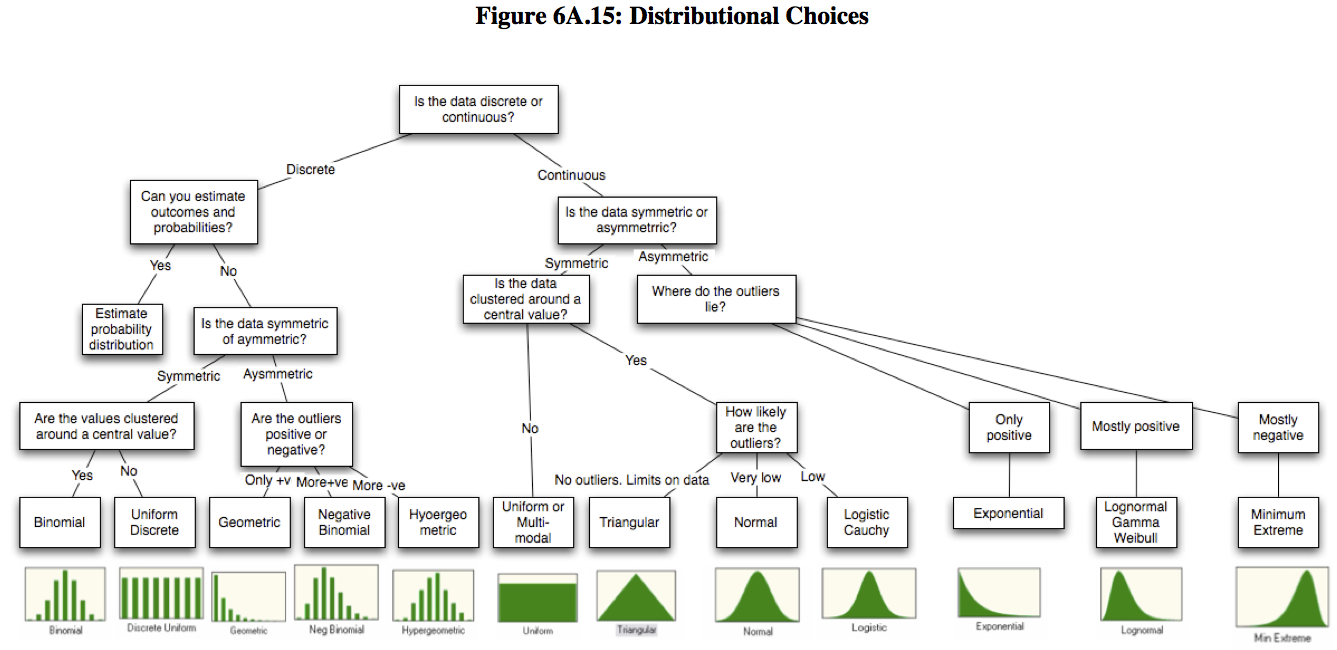
I came across the paper Probabilistic approaches to risk by Aswath Damodaran. In Appendix 6.1 Aswath discusses the key characteristics of the most common distributions and in Figure 6A.15 he provides a decision tree diagram for choosing a distribution:

Figure 6A.15 from Probabilistic approaches to risk by Aswath Damodaran

JD Long points to the Clickable diagram of distribution relationships by John Cook in his blog entry about Fitting distribution X to data from distribution Y . With those two charts I find it not too difficult anymore to find a reasonable starting point.

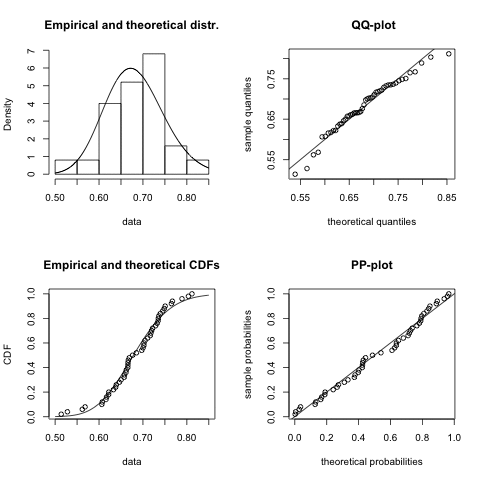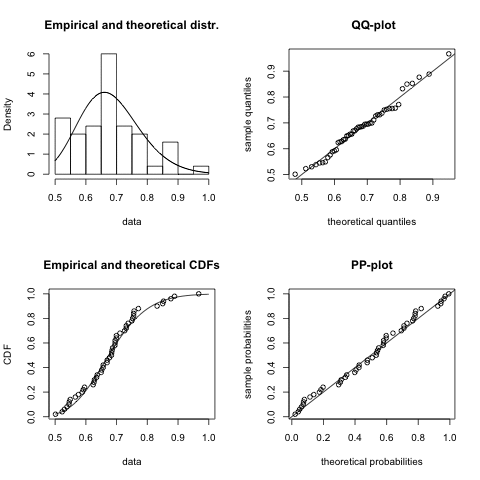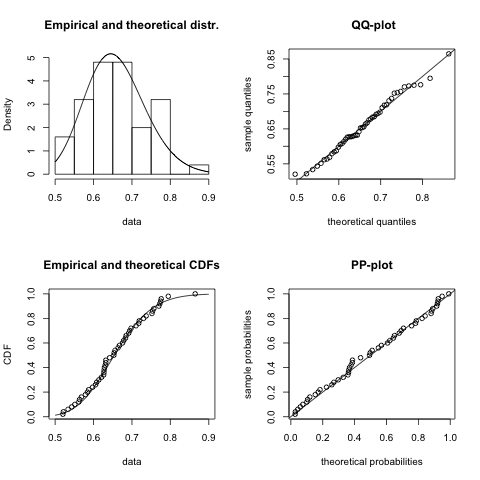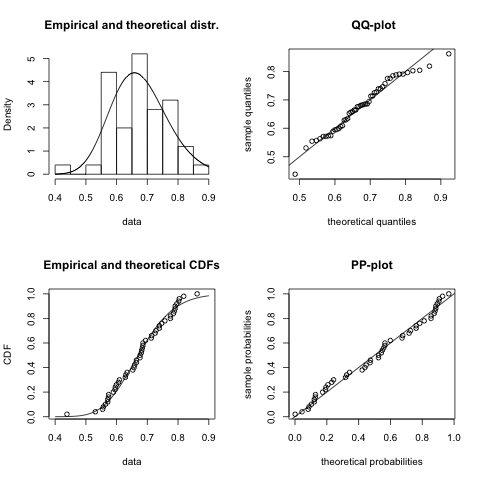
Once I have decided which distribution might be a good fit I start usually with the fitdistr function of the MASS package. However, since I discovered the fitdistrplus package I have become very fond of the fitdist function, as it comes with a wonderful plot method. It plots an empirical histogram with a theoretical density curve, a QQ and PP-plot and the empirical cumulative distribution with the theoretical distribution. Further, the package provides also goodness of fit tests via gofstat.

Suppose I have only 50 data points, of which I believe that they follow a log-normal distribution. How much variance can I expect? Well, let’s experiment. I draw 50 random numbers from a log-normal distribution, fit the distribution to the sample data and repeat the exercise 50 times and plot the results using the plot function of the fitdistrplus package.

I notice quite a big variance in the results. For some samples other distributions, e.g. logistic, could provide a better fit. You might argue that 50 data points is not a lot of data, but in real life it often is, and hence this little example already shows me that fitting a distribution to data is not just about applying an algorithm, but requires a sound understanding of the process which generated the data as well.